Python vs. Julia
Python vs. Julia
The SOC radiative transfer program was implemented as a combination of Python main program and OpenCL kernels, using the PyOpenCL library. Initial conversion to Julia language and the use of KernelAbstractions.jl library showed that the Julia option was at least 30% slower.
To understand this difference, we examined a smaller example that was reduced from original SOC code to about hundred lines of code, including one kernel and two other kernel-side routines. In addition to the Python+OpenCL and Julia+KernelAbstractions, we also included in the comparison Julia with the OpenCL.jl library, using the same OpenCL kernel as with PyOpenCL.
Here is the Python main program
#!/usr/bin/env python
import pyopencl as cl
from numpy import *
import time
import sys
t00 = time.time()
N = 128 # size of "density" grid
NRAY = 10000 # number of "rays"
USE_GPU = 1 # 0 = use CPU, 1 = use GPU
ATOMICS = 0 # 0 = no atomics, 1 = use atomic updates
if (len(sys.argv)>1):
USE_GPU = int(sys.argv[1])
ATOMICS = int(sys.argv[2])
if (USE_GPU>0):
GLOBAL = 1024
LOCAL = 32
platform = cl.get_platforms()[0] # test system "0" = POCL OpenCL
device = [platform.get_devices(cl.device_type.GPU)[USE_GPU-1],] # "0" = CPU
else:
GLOBAL = 32
LOCAL = 4
platform = cl.get_platforms()[1] # test system "1" = NVidia
device = [platform.get_devices(cl.device_type.CPU)[0],] # "0" = NVidia 5080 mobile
print(device)
context = cl.Context(device)
queue = cl.CommandQueue(context)
mf = cl.mem_flags
DENS = ones(N*N*N, float32) # Cartesian grid of N^3 cells, input "density"
DENS_buf = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR, hostbuf=DENS)
TABS = zeros(N*N*N, float32) # Cartesian grid of N^3 cells, kernel output
TABS_buf = cl.Buffer(context, mf.READ_WRITE, 4*N*N*N)
cl.enqueue_copy(queue, TABS_buf, TABS)
cl.enqueue_copy(queue, DENS_buf, DENS)
ARGS = " -D N=%d -D NRAY=%d -D ATOMICS=%d -D NVIDIA=%d" % (N, NRAY, ATOMICS, USE_GPU>0)
# ARGS += " -cl-mad-enable -cl-no-signed-zeros -cl-finite-math-only" # additional optimisation
source = open("kernel_test5.c").read()
program = cl.Program(context, source).build(ARGS)
kernel_test5 = program.test5
t0 = time.time()
for ifreq in range(10):
t1 = time.time()
kernel_test5(queue, [GLOBAL,], [LOCAL,], DENS_buf, TABS_buf)
cl.enqueue_copy(queue, TABS, TABS_buf)
print(" %.4f seconds" % (time.time()-t1)) # timing per kernel call
queue.finish()
print("%.4f seconds total, result %.3e" % (time.time()-t00, sum(ravel(TABS)))) # total time
and here the OpenCL kernel code
#define EPS 1.0e-4f
// #define ATOMICS 1
#if ATOMICS>0
#if (NVIDIA>0)
float atomicAdd_g_f(__global float* p, float val) {
float prev;
asm volatile(
"atom.global.add.f32 %0, [%1], %2;"
: "=f"(prev)
: "l"(p) , "f"(val)
: "memory"
);
return prev;
}
#else
inline void atomicAdd_g_f(volatile __global float *addr, float val) {
union{
unsigned int u32;
float f32;
} next, expected, current;
current.f32 = *addr;
do {
expected.f32 = current.f32;
next.f32 = expected.f32 + val;
current.u32 = atomic_cmpxchg( (volatile __global unsigned int *)addr,
expected.u32, next.u32);
} while( current.u32 != expected.u32 );
}
#endif
#endif
int Index(const float x, const float y, const float z) {
if ((x<=0.0f)||(y<=0.0f)||(z<=0.0f)||(x>=N)||(y>=N)||(z>=N)) {
return -1 ;
}
return (int)(floor(x)+N*floor(y)+N*N*floor(z)) ;
}
void Step(float *x, float *y, float *z, const float u, const float v, const float w, float *ds, int *ind) {
float s ;
s = (u>0.0f) ? ((1.0f+EPS-fmod(*x, 1.0f))/u) : ((-EPS-fmod(*x, 1.0f))/u) ;
s = min(s, (v>0.0f) ? ((1.0f+EPS-fmod(*y, 1.0f))/v) : ((-EPS-fmod(*y, 1.0f))/v)) ;
*ds = min(s, (w>0.0f) ? ((1.0f+EPS-fmod(*z, 1.0f))/w) : ((-EPS-fmod(*z, 1.0f))/w)) ;
*x += (*ds)*u ;
*y += (*ds)*v ;
*z += (*ds)*w ;
*ind = Index(*x, *y, *z) ;
}
_kernel void test5(__global float *DENS, __global float *TABS) {
const int id = get_global_id(0) ;
float x = 1.0f, y = 1.0f, z=1.0f, u, v, w, tmp, ds ;
int ind, oind ;
for(int iray=0; iray<NRAY ; iray++) {
u = x ; v = 0.1f ; w = 0.5f ;
tmp = sqrt(u*u+v*v+w*w) ;
u /= tmp ; v /= tmp ; w /= tmp ;
x = 39.5f ; y = 39.5f ; z = EPS ;
ind = Index(x, y, z) ;
while(ind>=0) {
oind = ind ;
Step(&x, &y, &z, u, v, w, &ds, &ind) ;
#if ATOMICS
atomicAdd_g_f(&(TABS[oind]), ds) ;
#else
TABS[oind] += exp(-ds) ;
#endif
}
}
}
The corresponding Julia main program, using the same c-language kernel, was
#!/usr/bin/env julia
using Printf
using Statistics
using OpenCL
const N = Int32(128)
const NRAY = 10000
t00 = time()
USE_GPU = 1
ATOMICS = 1
if (length(ARGS)==2)
USE_GPU = parse(Int32, ARGS[1]) # 0 = use CPU, 1 = use GPU
ATOMICS = parse(Int32, ARGS[2])
end
if (USE_GPU>0)
platform = cl.platforms()[1] # on test system "1" = NVidia
device = cl.devices(platform)[1] # on test system "1" = NVidia 4080 mobile
cl.device!(device)
GLOBAL = 1024
LOCAL = 32
else
platform = cl.platforms()[3] # on test system "3" = POCL OpenCL for CPU
device = cl.devices(platform)[1]
cl.device!(device)
GLOBAL = 32
LOCAL = 4
end
println(device)
fp = open("kernel_test5.c")
source = read(fp, String)
# P = cl.Program(; source) |> cl.build!
P0 = cl.Program(; source)
P = cl.build!(P0; options=@sprintf("-D ATOMICS=%d -D N=%d -D NRAY=%d -D NVIDIA=%d", ATOMICS, N, NRAY, USE_GPU))
K = cl.Kernel(P, "test5")
DENS = ones(Float32, N*N*N)
TABS = zeros(Float32, N*N*N)
D_DENS = CLArray(DENS)
D_TABS = CLArray(TABS)
function CL_test()
global DENS, TABS, D_DENS, D_TABS, LOCAL, GLOBAL
for ifreq=1:10
t1 = time()
clcall(K, Tuple{ CLPtr{Float32}, CLPtr{Float32}}, D_DENS, D_TABS; global_size=GLOBAL, local_size=LOCAL)
TABS = Array(D_TABS)
@printf(" %.5f seconds\n", time()-t1) # run time pre kernel call
end
end
CL_test()
@printf("%.4f seconds total -- result %.3e\n", time()-t00, sum(TABS)) # total run time
Finally, below is the entire Julia code using KernalAbstractions:
#!/usr/bin/env julia
using KernelAbstractions
const KA = KernelAbstractions
using Printf
# using Statistics
using Atomix
const N = Int32(128)
const EPS = 1.0f-4
const NRAY = Int32(10000)
t00 = time()
if (length(ARGS)==2)
const USE_GPU = parse(Int32, ARGS[1]) # 0 = CPU, 1 = GPU
const ATOMICS = parse(Int32, ARGS[2]) # 0 = no atomics, 1 = with atomic updates
else
const USE_GPU = false
const ATOMICS = false
end
if USE_GPU>0
using CUDA
using CUDA.CUDAKernels
BACK = CUDABackend()
CUDA.device!(0) # on test system "0" = NVidia 5080 mobile
println(CUDA.device())
CUDA.allowscalar(false)
const GLOBAL = Int64(1024)
const LOCAL = Int64(32)
else
BACK = CPU() # on test sytstem = POCL OpenCL on CPU
const GLOBAL = Int32(32)
const LOCAL = Int64(4)
end
const int0 = Int32(0)
const int1 = Int32(1)
@inline @inbounds function Index(x::Float32, y::Float32, z::Float32)::Int32
if ((x<=0.0f0)|(x>=N)|(y<=0.0f0)|(y>=N)|(z<=0.0f0)|(z>=N))
return int0
end
return Int32(1.0f0 + floor(floor(x)+N*floor(y)+N*N*floor(z)))
end
@inline @inbounds function Step(x::Float32, y::Float32, z::Float32, u::Float32, v::Float32, w::Float32)
ds = min(
(u>0.0f0) ? ((1.0f0+EPS-mod(x,1.0f0))/u) : ((-EPS-mod(x,1.0f0))/u),
(v>0.0f0) ? ((1.0f0+EPS-mod(y,1.0f0))/v) : ((-EPS-mod(y,1.0f0))/v),
(w>0.0f0) ? ((1.0f0+EPS-mod(z,1.0f0))/w) : ((-EPS-mod(z,1.0f0))/w)
)
x += ds*u
y += ds*v
z += ds*w
ind = Index(x, y, z)::Int32
return ds, ind, x, y, z
end
if (ATOMICS>0)
@kernel inbounds=true unsafe_indices=true function kernel_test5(@Const(DENS), TABS)
id = @index(Global, Linear) # 3.6 sec
id -= 1
x = 1.0f0 ; y = 1.0f0 ; z = 1.0f0 ; u = 0.0f0 ; v = 0.0f0 ; w = 0.0f0 ; ds = 0.0f0
for iray=1:NRAY
u = x ; v = 0.1f0 ; w = 0.5f0 ;
tmp = sqrt(u*u+v*v+w*w) ;
u /= tmp ; v /= tmp ; w /= tmp ;
x = 39.5f0 ; y = 39.5f0 ; z = EPS ;
ind = Index(x, y, z)::Int32
while(ind>=int1)
oind = ind
ds, ind, x, y, z = Step(x, y, z, u, v, w)
Atomix.@atomic TABS[oind] += ds
end
end
end
else
@kernel inbounds=true unsafe_indices=true function kernel_test5(@Const(DENS), TABS)
id = @index(Global, Linear) # 3.6 sec
id -= 1
x = 1.0f0 ; y = 1.0f0 ; z = 1.0f0 ; u = 0.0f0 ; v = 0.0f0 ; w = 0.0f0 ; ds = 0.0f0
for iray=1:NRAY
u = x ; v = 0.1f0 ; w = 0.5f0 ;
tmp = sqrt(u*u+v*v+w*w) ;
u /= tmp ; v /= tmp ; w /= tmp ;
x = 39.5f0 ; y = 39.5f0 ; z = EPS ;
ind = Index(x, y, z)::Int32
while(ind>=int1)
oind = ind
ds, ind, x, y, z = Step(x, y, z, u, v, w)
TABS[oind] += exp(-ds)
end
end
end
end
K_test5! = kernel_test5(BACK, LOCAL)
DENS = ones(Float32, N*N*N)
TABS = zeros(Float32, N*N*N)
D_DENS = KA.zeros(BACK, Float32, N*N*N)
D_TABS = KA.zeros(BACK, Float32, N*N*N)
KA.copyto!(BACK, D_DENS, DENS)
KA.copyto!(BACK, D_TABS, TABS)
function KA_test()
t0 = time()
for ifreq=1:10
t1 = time()
K_test5!(D_DENS, D_TABS, ndrange=(GLOBAL))
KA.copyto!(BACK, TABS, D_TABS)
# KA.synchronize(BACK)
@printf(" %.4f seconds\n", time()-t1) # run time per kernel call
end
end
KA_test()
@printf("%.4f seconds total -- result %.3e\n", time()-t00, sum(TABS)) # total run time
In each run with the above three programs (Python+OpenCL, Julia+OpenCL, Julia+KernelAbstractions) there are four variants, whether one uses CPU or GPU and whether the kernel makes updates using atomic operations or not. For correct results the updates should be atomic. However, since the implementations of the atomic operations are different (in particular, in the above OpenCL kernels implemented within the kernel and differently for CPU and GPU), we measured run times for comparison also without the atomics.
Each run includes initialisations and ten calls to the kernel routine. The following figure shows the run times (time per one kernel call), with the x-axis corresponding to the ten kernel calls included in one run. The first iteration(s) are affected by initialisation overhead (code compilation). For a short run (e.g. if run included only a single kernel call) the initialisation will be a significant part of the full run time. Conversely, the run times of the later iterations will be more representative of the relative performance in longer runs.
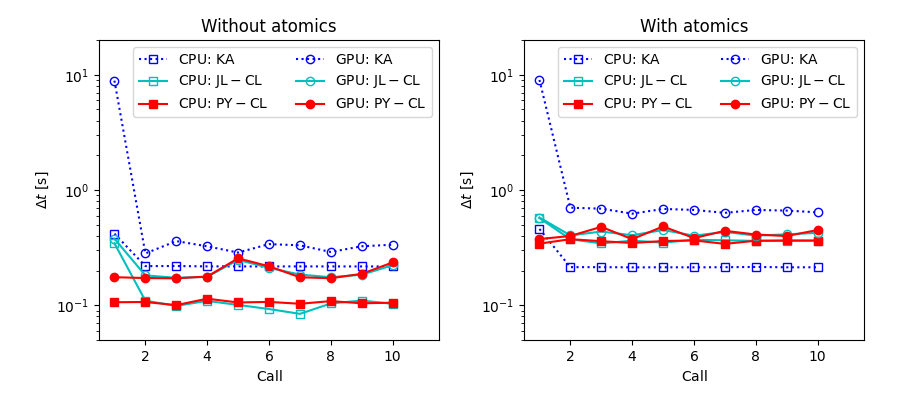
The Python and Julia OpenCL programs should have very similar timings because they share the same kernel code and the main programs stand for a small fraction of the run times. This is also the case, both on CPU and GPU. The first iteration takes longer in the Julia version (perhaps previously compiled kernel was not cached?).
On the other hand, the performance of Julia + KernelAbstractions shows clear deviations. Without atomics, it has the slowest performance. The difference is some 30% on GPU but on CPU the difference increases to more than a factor of two. In our previously tests with the SOC program, we found some 30% difference on both CPUs and GPUs.
In the version with atomic updates, the Julia + KernelAbstractions is on GPU still 30% slower than the OpenCL options - plus the initialisations continue to take a very long time (more than twice the OpenCL run times for the entire run with ten kernal calls). On the other hand, the use of atomic operations appears to have an almost negligeable effect on the CPU, where the KernelAbstractions version is now almost 50% faster than the OpenCL versions (if the slow initialisation are ignored…).
Based on the above, KernelAbstractions might be a good option for CPU calculations. However, as observed in tests with full SOC-program kernels, it can be (especially on NVidia) on GPUs unfortunately slower than OpenCL. The 30% difference is large anough to make one hesitate to commit to replacing Python + OpenCL with Julia + KernelAbstractions. There may not be a good reason for this performance difference, and one may hope that the situation will be improved by future library updates. Alternatively, it is possible that our KernelAbstractions implementation above is somehow flawed - in which case somebody will hopefully let us know how the performance could be improved (e.g. via GitHub, see below).
The tests were run on a laptop with Ultra 9 275HX CPUs (8+16 cores) and NVidia 5080 mobile GPU. The scripts can be found at GitHub , in the Julia_test subdirectory (test5.py for the python version, test5_cl.jl for the Julia OpenCL and test5.jl for the Julia KernelAbstractions version).